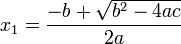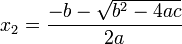Matematica I: abril 2014

BUENAS TARDES APRECIADOS ESTUDIANTES ANTE DE TODO RECIBAN UN CORDIAL SALUDO DE MI PARTE . LA SIGUIENTE PUBLICACIÓN ES PARA REFORZAR MAS EL CONTENIDO VISTO EL DÍA LUNES

Ecuación de Primer Grado

Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable, y que se cumple para determinado valor numérico de dicha incógnita.

Se denominan ecuaciones lineales o de primer grado a las igualdades algebraicas con incógnitas cuyo exponente es 1 (elevadas a uno, que no se escribe).

Como procedimiento general para resolver ecuaciones enteras de primer grado se deben seguir los siguientes pasos:

1. Se reducen los términos semejantes, cuando es posible.

2. Se hace la transposición de términos (aplicando inverso aditivo o multiplicativo), los que contengan la incógnita se ubican en el miembro izquierdo, y los que carezcan de ella en el derecho.

3. Se reducen términos semejantes, hasta donde es posible.

4. Se despeja la incógnita, dividiendo ambos miembros de la ecuación por el coeficiente de la incógnita (inverso multiplicativo), y se simplifica.

Resolución de ecuaciones de primer grado con una incógnita

Para resolver ecuaciones de primer grado con una incógnita, aplicamos el criterio del operador inverso (inverso aditivo o inverso multiplicativo), como veremos en el siguiente ejemplo:

Resolver la ecuación 2x – 3 = 53

Debemos tener las letras a un lado y los números al otro lado de la igualdad (=), entonces para llevar el –3 al otro lado de la igualdad, le aplicamos el inverso aditivo (el inverso aditivo de –3 es +3, porque la operación inversa de la resta es la suma).

Entonces hacemos:

2x – 3 + 3 = 53 + 3

En el primer miembro –3 se elimina con +3 y tendremos:

2x = 53 + 3

2x = 56

Ahora tenemos el número 2 que está multiplicando a la variable o incógnita x, entonces lo pasaremos al otro lado de la igualdad dividiendo. Para hacerlo, aplicamos el inverso multiplicativo de 2 (que es ½) a ambos lados de la ecuación:

2x • ½ = 56 • ½

Simplificamos y tendremos ahora:

x = 56 / 2

x = 28

Ejemplo

Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.

Quitamos paréntesis, agrupamos y sumamos los términos semejantes:

Despejamos la incógnita:

Ejercicios de ecuaciones lineales resueltos
1.

Una ecuación de segundo grado o ecuación cuadrática es una ecuación que tiene la forma de una suma de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un polinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática es:

$ax^2 + bx + c = 0, \quad \mbox{para}\;a\neq 0$

donde x representa la variable y a, b y c son constante; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede representar mediante una gráfica de una función cuadrática o parábola. Esta representación gráfica es útil, porque la intersección de esta gráfica con el eje horizontal coinciden con las soluciones de la ecuación (y dado que pueden existir dos, una o ninguna intersección, esos pueden ser los números de soluciones de la ecuación).

FÓRMULA CUADRÁTICA

De una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas. Se denomina fórmula cuadrática a la ecuación que proporciona las raíces de la ecuación cuadrática:

$x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}$

donde el símbolo ± indica que los valores

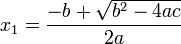$x_1 = \frac{-b + \sqrt {b^2-4ac}}{2a}$

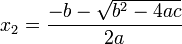$\ x_2 = \frac{-b - \sqrt {b^2-4ac}}{2a}$

constituyen las dos soluciones.

OTRA DEFINICIÓN DE LA ECUACIÓN

ECUACIONES DE SEGUNDO GRADO

Una ecuación de segundo grado o ecuación cuadrática es una ecuación que tiene la forma de una suma de términos, todos ellos con potencias a los más de segundo grado, es decir, una ecuación cuadrática puede ser representada por un polinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática es:

$ax^2 + bx + c = 0, \quad \mbox{para}\;a\neq 0$

donde x representa la variable y a, b y c son constantes; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede representar mediante una gráfica de una función cuadrática o parábola. Esta representación gráfica es útil, porque la intersección de esta gráfica con el eje horizontal coinciden con las soluciones de la ecuación (y dado que pueden existir dos, una o ninguna intersección, esos pueden ser los números de soluciones de la ecuación).